Classical and Quantum superintegrable systems
Due to their remarkable properties the search and classification of classical and quantum superintegrable systems, systems that allows more integrals of motion than degrees of freedom, is of great interest in different branches of Physics. They are related with the notion of exact solvability and serves as zero order approximation in perturbation theory for more elaborate models. Interestingly, classical and quantum superintegrable potential can differ. The relation between superintegrability and the classification of orthogonal polynomials is overwhelming.
Fluctuations in quantum mechanics and field theories, with A. Turbiner (UNAM) and E. Shuryak (Stony Brooke)
Semiclassical approximations are well known tools, both in quantum mechanics and quantum field theory. Standard textbooks of quantum mechanics usually start with the Bohr-Sommerfeld quantization conditions and the semiclassical WKB approximation for the wave function. Unfortunately, extending such methods beyond the first correction for the one-dimensional case or those with separable variables, or to a multidimensional case, proved to be difficult. In mathematical physics, general constructions for multidimensional complexified saddle points are related to their extrema and the network of the so-called Lefschetz thimbles (solutions of the gradient flow equations) connecting them. Applications of such a theory in the path-integral context have been investigated by Witten, which inspired a number of subsequent studies. Semiclassical methods that start with Feynman path integrals, on the other hand, are applicable not only for many dimensions or many-body applications, but even for quantum field theories. The so-called instanton calculus has been developed for gauge theories and other models. Instantons are indeed responsible for many important phenomena in quantum field theories (QFTs). From a technical point of view, however, so far the calculations have not progressed beyond one loop in any of these QFT applications.
General classical and quantum N-body system (with A. Turbiner, ICN-UNAM)
By experience we know that the ground state (and some other states) of the system of n bosons depend on relative distances only. What is the equation in the space of relative distances if exists which describes ground state (and other states without angular dependences)? It is known that in general there is no separation of relative distances from relative angular variables in the space of relative motion. Is there a way to separate relative distances from relative angles to reduce effectively the dimensionality of the original problem? What are the most convenient variables to parametrize the space of relative distances?
Algebraic and perturbative methods in atomic physics
The behavior of a charged particle in a constant magnetic field (the Landau problem) is well studied. It is an integrable and exactly-solvable problem, both classical and quantum and it plays a fundamental role in physics. The problem of two of more charges in a magnetic field is much less studied, while most of the effort has been dedicated to explore the case when one charge is infinitely massive (the one-center problem).The n-body closed chain of harmonic oscillators
The two-body harmonic oscillator, namely two particles with masses m1 and m2 interacting via the potential V ∝ |r1 − r2 |^2, appears in all textbook in Classical Mechanics. In an arbitrary d−dimensional Euclidean space R^d this system admits separation of variables in the center-of-mass and relative coordinates as well as exact solvability. The relevance of such a system is obvious: any scalar potential U = U(|r1 − r2 |) can be approximated near its equilibrium points by the two-body harmonic oscillator. In this case, the center of- mass and relative coordinates are nothing but the normal coordinates. Therefore, in the n-body case of n > 2 particles interacting by a generalized quadratic pairwise potential it is natural to ask the question about the existence of normal coordinates and the corresponding explicit exact solutions. Interestingly, even for the three-body case n = 3 a complete separation of variables can not be achieved in full generality and the system becomes chaotic.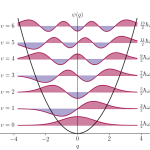
Dynamical systems & Artificial Intelligence (with Mario Alan Quiroz, CFATA-UNAM)
We study the reconstruction of dynamical governing equations from series data, dynamics of classical Hamiltonian systems as well as quantum chaos using IA algorithms.
